Hellow everyone,
I am working for a humanitarian organisation in an internally displaced persons camp in South Sudan. The camp has about 100,000 people. We know that there have been a few different campaigns in recent months to improve the vaccination coverage for polio and measles. However, the campaign data appears to be a bit unreliable compared to the population data that we have. Therefore, we would like to implement a vaccination coverage survey to estimate the proportion of children between 6 months and 5 years that are currently immunised for polio and measles. We calculated a sample size of approximately 400 children that we need to include in the survey to estimate the coverage. We are now wondering what sampling techniques we should use to implement this survey. Do you have any advice?
Thank you for your suggestions
Considering you are working in a closed setting, you have a few options for the sampling approach you can take. The one you choose will depend a bit on the resources you have to implement the survey and how quickly it needs to be implemented. In an ideal scenario, you will want to choose a sampling method that approaches simple random sampling as much as possible (as simple random sampling is the gold standard for survey sampling). But there are other ways. I have outlined the options you have with their advantages and disadvantages below:
- Exhaustive sampling: this is the most logistically difficult and resource intensive. Your aim would be to include every child in the camp in the target age group in your sample. The easiest way to achieve this would be to go from household to household in the camp. The risk with it is that you end up double counting children and perhaps even lose track of which households you have included. For this sampling approach you would not require the sample size calculation you conducted as you would include all children in the camp in your target group.
- Convenience sampling: this is the easiest and fastest one to implement, but the risk is that you introduce a lot of bias depending on where you sample. You could for example park yourself in the outpatient department of the health facility of the camp and sample 400 children that attend the clinic. This would be easy to do, it is likely that parents or caregivers bringing their children would carry with them all 1. available medical documentation they have on the children (including vaccination cards). The problem with this approach is that you are sampling from a group of households that are likely to bring their children to receive healthcare (thus possible more inclined also to accept that they are vaccinated). Sometimes you might have to compromise on scientific robustness to get quick estimates for vaccination coverage. In those instances, convenience sampling is a great approach as long as you are aware and vocal about the limitations in the biased sample you have used.
- Systematic sampling: this approach requires that you first calculate how many households you will have to visit in the camp in order to achieve your sample size of 400 children. Lets assume that the average household size is 5 people in the camp in which you work (for ease of calculation). Of those 5 people per household there are probably around 20% aged 6 months to 5 years (double check these assumptions with your own data on your population). Thus 1.15 persons per household are in your target age group. In order to reach the sample size of 400, you will need to visit 348 (400/1.15) households. There are approximately 20,000 households in the camp (100,000/5 people per household). Your sampling fraction for your systematic sampling therefore is 20,000/348=57. You would therefore need to sample each 57th household and sample all the children in that household in order to reach your sample size. You would therefore need to choose a random starting household (random number between 1 and 57) on one end of the camp, and then select every 57th household until you had covered the whole camp and reached your sample size. This sampling approach is easy to do if your camp is well organised in straight rows/streets, so survey teams have an easy time identifying each 57th household. If the camp is not well organised, this sampling approach will be difficult to implement and you will risk double surveying multiple households.
- Simple random sampling: this is the gold standard of sampling in which each individual in your target population should have an equal probability of being included in the study sample. To be able to do this correctly, you should be able to have a list of all individuals in your target population available and select survey participants from this list at random. For example, if you had a population register for all children aged 6 months to 5 years and numbered, you would generate 400 random numbers and visit each of the 400 children you selected in that way. This is unlikely to be feasible, so you generally try and visit randomly selected households to achieve your sample size. We calculated earlier that this would be 348 households to see 400 children. Thus you will need to randomly sample amongst the household in your camp. If you have a list of the 20,000 households, you could randomly select 348 from this list. Alternatively, you could use GPS-based sampling, generate 348 random GPS points within the confines of the IDP camp, and visit the households closest to those GPS points.
- Cluster based sampling: this approach would generally not be used inside a closed setting like a camp. Generally your sample size will need to be increased in order to account for the sampling design.
1 Like
Thank you for this very detailed explanation! There are times I work in closed or humanitarian settings and this is very useful. Could you elaborate a little more on GPS-based sampling? Would there be some sort of design effect that you would have to adjust, for example unequal density of households in different parts of the camp? How would you generate random GPS points? If this requires a software, I would appreciate linking to some resources.
Dear @iancgmd,
Find below how you might attempt to do the GPS based random sampling that has been stated in point 4 by @jcfernandezm.
A similar approach in Qgis 4.2 Spatial random sampling with QGIS | Technical Guide for Estimating Building Rooftop Solar Potential in a City
I hope this is helpful.
library(sf)
library(dplyr)
library(reprex)
nc = st_read(system.file("shape/nc.shp", package="sf"))
#creating an example camp boundary, since I do not have access to your camp
#boundary. This could be replaced by your actual camp boundary
camp_boundary_polygon <- nc %>%
filter(NAME == "Ashe") %>%
st_geometry()
#Object class should be sf polygon
class(camp_boundary_polygon)
#> [1] "sfc_MULTIPOLYGON" "sfc"
#Now,taking a random sample of points from within the boundaries of a polygon boundary,
#I have taken 50, for illustration, but you are looking for 348 points so you could change the size to 348
random_spatial_rnd_pts <- st_sample(camp_boundary_polygon, size = 50, type ="random")
plot(camp_boundary_polygon)
plot(random_spatial_rnd_pts, add = TRUE, col = "red")
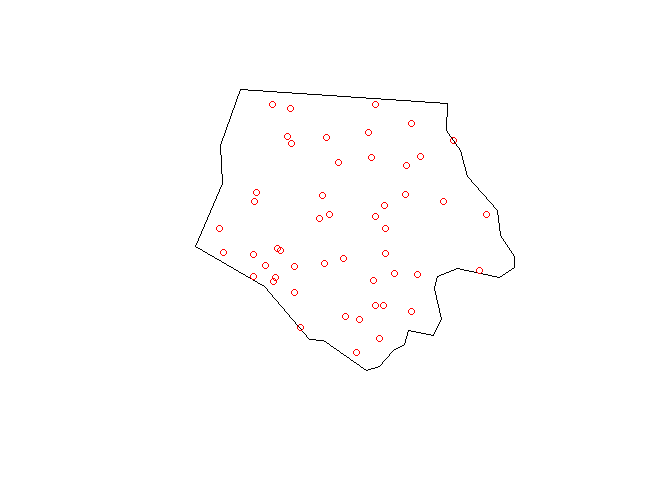
st_write(random_spatial_rnd_pts, dsn = "random_spatial_rnd_pts.shp")
#You could then take the sampled spatial points that have been exported by st_write and load them into a GPS device,
#the next step would be to trace the physical location of the points using the GPS device, the houses that
#will be selected for participation in the survey will be the one's closest to each of the
#spatial point.
Created on 2022-05-09 by the reprex package (v2.0.0)
1 Like
Thank you for this! Just to clarify, the shapefile should be the polygon for the camp boundary, correct?
Yes exactly, the polygon should be the camp’s boundary thanks. Good luck!
1 Like
